2023-06-06
カテゴリー:中学入試に役立つ学習法:算数編
今日は「分数の計算」の最後となる、「部分分数分解」について書いていきます。この単元は、本来ならば高2で学習する「数B」の数列の範囲に含まれる内容なのですが、中学入試では「計算の工夫」の一部として頻出単元に含まれます。
基本パターンは誘導部分なしに出題され、応用パターンは誘導部分から類推して計算を工夫する問題となっています。中学受験生にとっては「知識として知らないと解けない分野」になるため、しっかりと解き方を覚えておきましょう。
部分分数分解の基本パターン
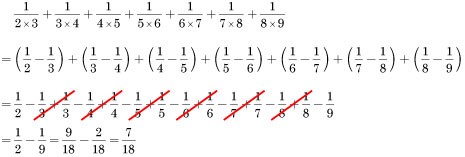
パターン①:分母が連続する2整数の積である場合(分母に積の表記がある場合)
パターン①の応用:分母が連続する2整数の積である場合(分母に積の表記がない場合)
パターン②:分母が連続する3整数の積である場合(分母に積の表記があり、分子が1の場合)
パターン②の応用:分母が連続する3整数の積である場合(分母に積の表記があり、分子が1以外の整数の場合)
パターン③:分母が等差の2整数の積である場合
パターン④:分母が等差の3整数の積である場合
このように、難解な内容ですがしっかり覚えておきましょう。というわけで、今日はここまでにします。
2023-05-17
カテゴリー:中学入試に役立つ学習法:算数編
前回は「循環小数と分数」の関係についてでしたが、その中で「分数の計算」には3種類の難問があると書いたのを覚えているでしょうか。今回はその中のひとつ「繁分数(はんぶんすう)」の計算について書いてみたいと思います。繁分数の計算は、分数の基本的な計算概念に基づけば難しいものではありませんから、はじめて見たときにはどうやって解いたらいいのか戸惑いますが、きちんとできるようにしましょう。
例を挙げて説明しましょう。繁分数というのは、分母や分子が分数であるような分数のことですから
のような分数です。分数の基本は分子÷分母ですから、上の問題は、
1÷(1+2分の1)=1÷2分の3=1×3分の2=3分の2
が答えになります。ですから、
のような問題では、
3÷(1+1÷□)=2.5
という問題を解くのと同じなわけです。では、次のような問題はどうやって解くのでしょう。
A〜Dにあてはまる整数を答えなさい。
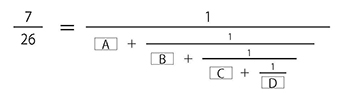 (早大学院高)
(早大学院高)
26を7で割ると3あまり5ですから、
になりますよね。ですから、Aは3になります。そしてBは1.4の整数部分にあたる1になるわけです。 さらにこれを続けて解いていくと、A=3、B=1、C=2、D=2となります。「分数の計算」についての話も次回が最後になります。もう少しですから頑張りましょう。というわけで、今日はここまで。
2023-04-25
カテゴリー:中学入試に役立つ学習法:算数編
今日は「分数の計算」の中でも、3種類の難問のうちの1つにあたる、「循環小数と分数」の関係について書いてみたいと思います。これは、本来は高1で学習する数Ⅰで習う内容なのですが、難関中学や難関高校の入試問題では、問題の最初に誘導部分をつけて出題される分野であり、難関中学を目指す小学生は理解しておくべき単元です。
さて、算数編その9で書いたように、小数はすべて分数で表すことが可能です。小数の中でも、0.1111・・・・・や0.3333・・・・や0.123123123・・・・のように同じ数字が繰り返しあらわれる数を循環小数と呼ぶのですが、これらの小数を分数に表すにはどうすれば良いのでしょう。
まず、循環小数の基本について学びましょう。
0.1111・・・・・という数は、
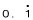
のように書き表し、
9分の1になります。つまり、
1を9で割っていくと0.1111・・・・・となりますよね。同様に、
0.010101・・・・・という数は
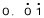
のように書き表し、
99分の1になります。
1を99で割ると0.0101・・・・・になるでしょ。これらをまとめると、
となります。そこで、これらの基本となる数をもとにして考えると、
のようになります。したがって、
のようにちょっと複雑な循環小数であっても分数に直すことができます。では、0.0111・・・・・はどうすれば良いのでしょう。
とやはり分数にすることができます。というわけで、「循環小数と分数」の関係について理解できたでしょうか。それでは、今日はここまでにしましょう。
2023-03-28
カテゴリー:中学入試に役立つ学習法:算数編
やっと公約数や公倍数の基本的な部分が終わったので、これから「分数の計算」について書いていきたいと思います。
そこで、「まず分数とは何か?」という基本から始めたいと思います。一言で言えば、「分数とは分子を分母で割った数」のことです。
小学校に入ってまず最初に習うのが整数ですよね。次に習うのが小数です。そして最後に習うのが分数なのですが、これら3種類の数を難しい言葉で「有理数(ゆうりすう)」と呼びます。有理数の反対語は、「有」の字を「有」の否定語である「無」に変えた、「無理数(むりすう)」になります。
小学生の皆さんには、「無理数」というのはあまりなじみの無い言葉かもしれませんが、円周率や平方根などが無理数にあたります。円周率が3.141592653589793・・・と無限に続く数であるということは聞いたことがあるでしょう?実は、無理数というのは「分数で表すことができない数」のことなのです。つまり無理数というのは、「分子を分母で割ることが無理な数」のことです。
したがって、有理数というのは「分子を分母で割ることができる数」のことですから、整数や小数は必ず分数で表すことができるのです。ところが3分の1という数を小数で表すと、0.3333333・・・・・となってしまいますし、9分の1は0.111111・・・・・、37分の21は0.567567567・・・・・となってしまい、分数は必ずしも小数で表せませんよね。だから分数は便利なのです。
というわけで、基本的な計算問題は小数を分数に直して計算するのが望ましいのです。
例を挙げて説明しましょう。
(0.75÷0.2+0.375―6分の1+0.625×0.5)×15分の4を計算しなさいという問題では、
0.75を4分の3
0.2を5分の1
0.375を8分の3
0.625を8分の5
0.5を2分の1
に変えて計算するわけです。したがって、良く出る小数はすぐに分数に変換できるように暗記しておくべきです。
では暗記しておくべき小数はというと、
0.5=2分の1
0.2=5分の1
0.4=5分の2
0.6=5分の3
0.8=5分の4
0.25=4分の1
0.75=4分の3
0.125=8分の1
0.375=8分の3
0.625=8分の5
0.875=8分の7
上に挙げた11個だけ覚えておけば、計算の早業ができますので、しっかり覚えておきましょう。それでは、今日はこのへんで終わりにしましょう。
(計算の答えは1と36分の5です)
2023-03-07
カテゴリー:中学入試に役立つ学習法:算数編
今日は「分数の計算」に入る前の最後の確認事項として、整数どうしの最小公倍数や最大公約数を見つけるための基本法である、「連除法」について書いてみたいと思います。
①2つの整数の最大公約数、最小公倍数の見つけ方
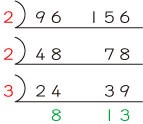
たとえば、96と156の最大公約数と最小公倍数を見つけるには、96と156の両方を割ることのできる整数で次々に割っていきます。
となり、8と13は1以外の約数を持ちません(互いに素と呼びます)から、もう割れませんね。
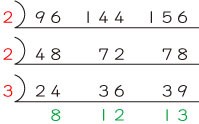
このとき、96と156を割った数の2と2と3をかけた数、すなわち12が96と156の最大公約数になります。また、最大公約数の12に8と13をかけた数、すなわち1248が96と156の最小公倍数になります。ここまでは、「そんなの、わかっているよ」というところですよね。では、3つの整数ではどうでしょうか。96と144と156の3つの整数の最大公約数と最小公倍数を同じように求めてみましょう。
②3つの整数の最大公約数、最小公倍数の見つけ方
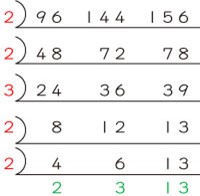
さて、この時点で8と12と13は互いに素(1以外に約数を持たない)になりましたから、やはり最大公約数は2×2×3=12です。では最小公倍数は、12×8×12×13=14976なのでしょうか。違いますよね。3つ以上の整数の最小公倍数を求めるときには、さらに割る必要があるんでしたよね。つまり、
まで割って、2×2×3×2×2×2×3×13=3744が96と144と156の最小公倍数です。もちろん、最大公約数は2×2×3×2×2=48ではなく、上で求めたように12ですよ。
このように、2つの整数の最大公約数・最小公倍数の連除法と3つ以上の整数の最大公約数・最小公倍数の連除法は、すこし違うことに注意しましょう。これを同じようにやってしまって間違える生徒は多いですからね。それでは、続きはまた。
2023-02-14
カテゴリー:中学入試に役立つ学習法:算数編
今日は約数の個数について書いていきます。前回は「エラトステネスの篩(ふるい)と素数」について書いたわけですが、すべての整数は素数の積で書き表すことができます。そして、整数を素数の積で表すことを「素因数分解」と呼びます。この素因数分解はとても大事な概念であり、昔は小学校で習い、少し前は中1で、今では中3の最初に習います。
ということは、小学生は分数の通分や約分を「何となく」やっているわけです。ですから小学校では、答えを既約分数(それ以上約分できない分数)で答えなくてもマルなのです。「えっ、そうだったの」と思われる方も多いと思いますが、それが日本の標準的な教育であるということを親が認識しておかないと、子どもとしては理不尽に注意された気になりますから注意してください。ただし分数の約分や通分を学習するのは、小学校では6年生になってからですから・・・・・普通に小学校の進度で勉強していたら中学入試には間に合わないわけで・・・・・だから中学受験的には4年生の2学期には分数の計算をできるようにしてしまうわけです。
というわけで、今日の本題である約数の個数の話に行きましょう。
(3)「約数の個数」について
「48の約数の個数は何個ですか」という問題を解くと、48という整数は
1×48
2×24
3×16
4×12
6×8
のように表すことができますから、48の約数は、1,2,3,4,6,8,12,16,24,48の10個です。このぐらいの大きさの数ならば、このように書いていったほうが間違えませんよね。
じゃあ「3024の約数の個数は何個ですか」という問題を同じように解くと、
1×3024
2×1512
3×1008
4×756
6×504
7×432
8×378
9×336
・
・
・
もうやめましょう・・・・・時間と行数ばかりかかります。う〜ん、一発で出す方法はないかなあ、となりますね。実はあるんです。
3024を素因数分解すると、2×2×2×2×3×3×3×7ですから、2を4個、3を3個、7を1個かけた数ですよね。ですから、3024の約数の個数は
(4個+1)×(3個+1)×(1個+1)=5×4×2=40個
このやり方は高校数学では定番なのですが、中学入試でも上位難関校では出題されることがあります。きちんとした理屈は「式の展開」という方法を習ってからでないとわからないのですが、覚えておいて損はない方法です。この方法を48にあてはめて解いてみると、48=2×2×2×2×3ですから、2を4個、3を1個かけた数なので、48の約数の個数は、
(4個+1)×(1個+1)=5×2=10個
数え上げなくても約数の個数がわかります。というわけで、難しい話になりましたが、難関中学受験生は覚えておいてください。では、今日はこの辺で。

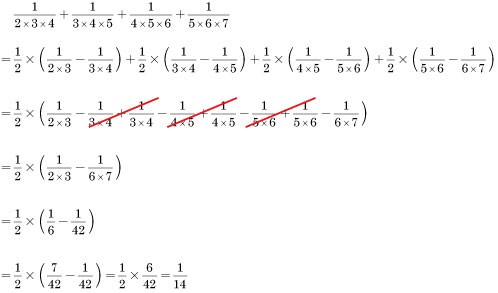

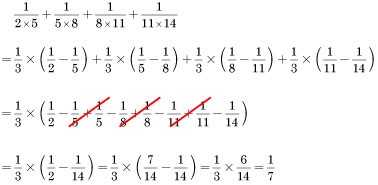
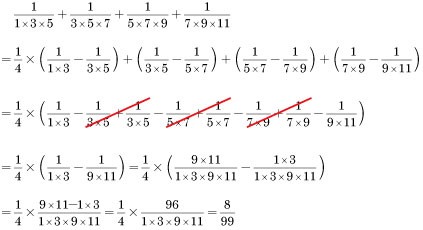


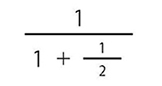
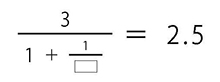
 (早大学院高)
(早大学院高)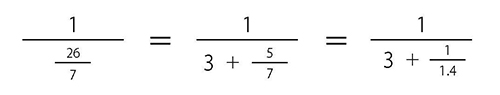
 のように書き表し、
のように書き表し、 のように書き表し、
のように書き表し、
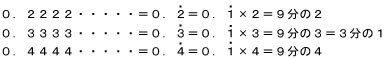
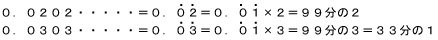
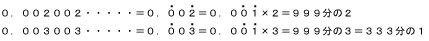
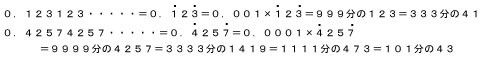
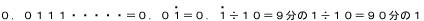
 お問い合わせフォーム
お問い合わせフォーム