2023-03-09
エクセレントゼミナールでは、本年度も「難関中日本史の征服講座」を4月〜7月の毎土曜10:30〜12:00、全14回で開設いたします。
最近の難関中の出題傾向を分析すると、難関中学になればなるほど社会の設問の難度が上がっています。特に社会科の入試問題の4割を占める日本歴史の分野に関しては、大学入試レベルの知識(大学入試共通テストレベル)がなければ解答できない設問も多くみられます。ところが、それら難関中学の合格者(受験者の大多数が御三家中併願者)の社会の得点率は85%に上ります。
つまり、中学受験の社会科においては、細かな学習知識が不足している受験生は難関中学の合格者になれないのです。
だから、エクセレントゼミナールでは、難関中学の出題レベルに対応するために、大学入試レベルをカバーする日本史の講座(4月15日〜7月15日の毎土曜10:30〜12:00の全14回、38500円税込、1回(4400円税込)ごとの申し込みも可能)を設置いたしました。テキストはオリジナルのテキストを使用し、カリキュラム進度は予習シリーズ5年下に準じるものとします。 小6の難関中受験者レベルに対応した内容ですので、受講にあたっては一通り日本史を学習した6年生が望ましいですが、秋に学習する日本史を先取り学習したい5年生も受講可能といたします(講座定員12名)。高い志を持つ受験生の受講を望みます!!
2023-03-07
カテゴリー:中学入試に役立つ学習法:算数編
今日は「分数の計算」に入る前の最後の確認事項として、整数どうしの最小公倍数や最大公約数を見つけるための基本法である、「連除法」について書いてみたいと思います。
①2つの整数の最大公約数、最小公倍数の見つけ方
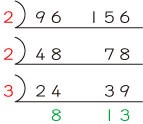
たとえば、96と156の最大公約数と最小公倍数を見つけるには、96と156の両方を割ることのできる整数で次々に割っていきます。
となり、8と13は1以外の約数を持ちません(互いに素と呼びます)から、もう割れませんね。
このとき、96と156を割った数の2と2と3をかけた数、すなわち12が96と156の最大公約数になります。また、最大公約数の12に8と13をかけた数、すなわち1248が96と156の最小公倍数になります。ここまでは、「そんなの、わかっているよ」というところですよね。では、3つの整数ではどうでしょうか。96と144と156の3つの整数の最大公約数と最小公倍数を同じように求めてみましょう。
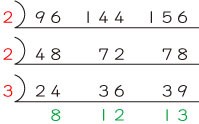
②3つの整数の最大公約数、最小公倍数の見つけ方
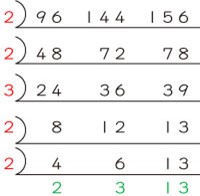
さて、この時点で8と12と13は互いに素(1以外に約数を持たない)になりましたから、やはり最大公約数は2×2×3=12です。では最小公倍数は、12×8×12×13=14976なのでしょうか。違いますよね。3つ以上の整数の最小公倍数を求めるときには、さらに割る必要があるんでしたよね。つまり、
まで割って、2×2×3×2×2×2×3×13=3744が96と144と156の最小公倍数です。もちろん、最大公約数は2×2×3×2×2=48ではなく、上で求めたように12ですよ。
このように、2つの整数の最大公約数・最小公倍数の連除法と3つ以上の整数の最大公約数・最小公倍数の連除法は、すこし違うことに注意しましょう。これを同じようにやってしまって間違える生徒は多いですからね。それでは、続きはまた。


 お問い合わせフォーム
お問い合わせフォーム